This lesson is adapted from my post Skynet’s Already A Better Dad Than Me
Start with a math puzzle from Martin Gardner’s Entertaining Mathematical Puzzles:
THE SILVER BAR A silver prospector was unable to pay his March rent in advance. He owned a bar of pure silver, 31 inches long, so he made the following arrangement with his landlady. He would cut the bar into smaller pieces. On the first day of March, he would give the lady an inch of the bar, and on each succeeding day he would add another inch to her amount of silver. She would keep this silver as security. At the end of the month, when the prospector expected to be able to pay his rent in full, she would return the pieces to him.March has 31 days, so one way to cut the bar would be to cut it into 31 sections, each an inch long. But since it required considerable labor to cut the bar, the prospector wished to carry out his agreement with the fewest possible number of pieces. For example, he might give the lady an inch on the first day, another inch on the second day, then on the third day he could take back the two pieces and give her a solid 3- inch section. Assuming that portions of the bar are traded back and forth in this fashion, see if you can determine the smallest number of pieces into which the prospector needs to cut his silver bar.
[They will fumble with the problem but let it simmer and say you’ll come back to it much later]
Then explain that by the time they are done they will be able to spell any word with one hand!
Proceed to the lesson:
The Basic Lesson
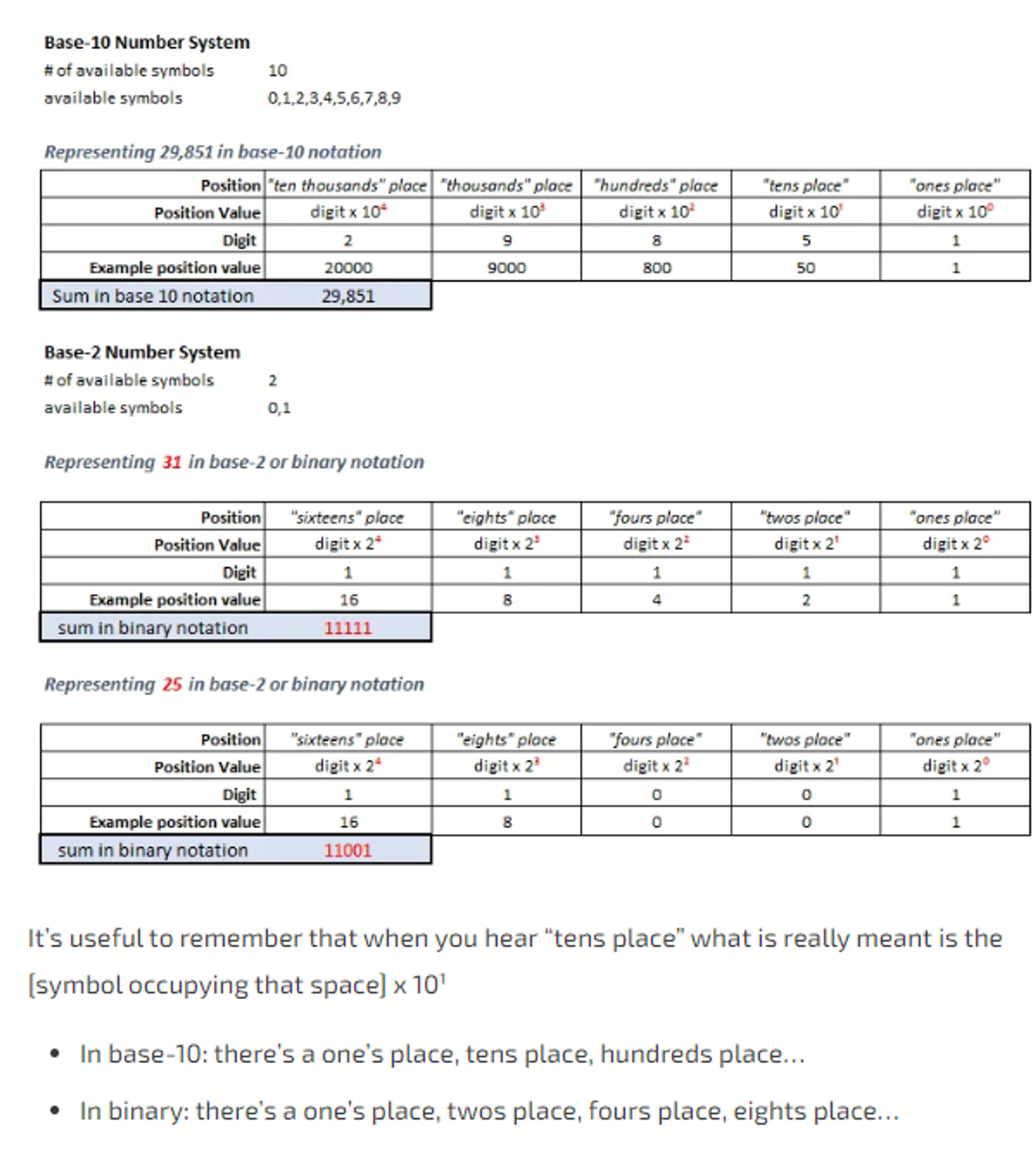
- Pick a 4-digit number and break it down in base 10 (highlight how many symbols were available to us and how in base 10 the highest symbol is 9 and in base-5 the highest symbol is 4)
- Then we do the same thing in binary ie base-2. Break down the number “44”
Use this chart to understand the concept yourself so you can be a guide:
Extend the Lesson
- Represent “44” in base-6
- Represent the current year in base 5
- Show how you can represent any number up to 63 on one hand in binary
- Spell their name in binary using a cipher (ie A = 1, B = 2…Z = 26)
- Bridge this to ASCII so they understand that physical inputs like a keyboard stroke is converted to binary which a processor can understand! Computers do calculations in binary because electrical signals on a chip are either on or off. So representing numbers can be thought of like a morse code of “on”/”off” at light speed or something.