Introduction
On August 5th 2022, this tweet appeared on my timeline:
The tweet asserts that the LEAPs are expensive or “priced for perfection”. The next part of the sentence is shaky if you take it literally — “if you can hedge the upside blowout risk”. You “can” sell the straddle for about $50 whether or not you can hedge the upside, but the author is prudently demonstrating where the risk resides. I give a total hall pass to the writing as my own tweets are often thrown together while standing in line at Trader Joe’s.
Allow me to re-word the tweet without worrying about character limits and without feeling rushed.
“Optically, the CVNA LEAP straddle is expensive because it’s trading for the same premium as the strike price. I can’t get burned on the downside so my only concern is the unbounded upside of the call option I’m short, so if I can truncate the potential loss there, this straddle is a good candidate to sell”
The original poster exhibits a solid understanding of options. But…markets are hard. They don’t leave free or near-free money laying around. It turns out, with 5 months of hindsight, this is a good case study in the limits of optically attractive trades.
[In What The Widowmaker Can Teach Us About Trade Prospecting And Fool’s Gold I dissect another optically attractive trade that is really just fool's gold.]
By dissecting what has happened we can learn about how to think of options “dynamically”.
We’ll use a rhetorical approach to this lesson to make it more interactive. Think about your answers before toggling open the answer or discussion.
Building An Understanding Of A Short Option Trade
On August 5, 2022 CVNA closed at $46.98
Assumptions
- For all questions assume zero carry costs. This is a non-dividend paying stock and we assume borrow and lend rates are 0%
- The original tweet referred to LEAPs which are long-dated options. The tweet was referring to the January 19, 2024 expiry. On 8/5/2022, this option had 532 calendar days to expiry (”DTE”)
- We will be focusing on the $50 strike, the same strike the tweet referred to.
- All of our hypothetical trades occur at closing marks.
- Anytime I use an option calculator, I am assuming European-style exercise. This means the option cannot be exercised early. This assumption is convenient for 2 reasons
- The calculator I use in Excel is a simple Black-Scholes model.
- The tweet discussed selling the straddle. The European-style straddle cannot be worth more than the American-style so we are being maximally conservative. In other words, the analysis that follows is only stronger with such an assumption since in real life, the tweet referred to a listed equity option which is American-style exercise.
- If CVNA is trading $46.98 What is the maximum value of the $50 strike straddle?
- Imagine you sell the $50 strike call for $48 and hedge by buying the stock for $47. If the stock goes to zero or $500 the result is the same. You make $1 profit.
- You sold the 50 strike call for $48.
- Carry cost = 0
- Intrinsic for a put = strike price - stock price = $50 - $47 = $3
Answer
The maximum value of the $50 strike put is $50. If the stock goes to 0, the put is worth $50. This is an arbitrage bound.
The maximum value of the $50 strike call is $46.98.
Why?
It’s also an arbitrage bound!
💻 Computations: Working out the cash flows to understand arbitrage
If you sell any call option for more than the stock price you cannot lose if you hedge the call option on a 100 delta.
Put-Call Parity Equation
Put = Intrinsic + Call - Carry Cost
If you sell a call and hedge by buying stock on a 100% delta or trader lingo “1-to-1”, then you have turned a short call into a synthetic short put.
In this example, you have sold the 50-strike put for $51 when the most it can be worth is $50.
Let’s step through it to see why:
50 Strike Put = Intrinsic + 50 Strike Call - Carry Cost
50 Strike Put = $3 + $48 - $0
50 Strike Put = $51
Since this put cannot be worth more than $50, you have made a $1 arbitrage profit.
By selling any call option by more than the stock price and hedging, you are selling the equivalent strike put for more than the put’s maximum value (ie the strike price)!
Max straddle value = max value of the call + max value of the put
Max straddle value = $46.98 + $50
Max straddle value = $96.98
So this “priced for perfection” or “priced to sell straddle” appears very fat because it’s trading for $50 but that is only near the maximum value of the call or put.
It’s still $46.98 cheaper than its arbitrage maximum value.
That said, the fact that it’s not trading near its maximum value doesn’t mean it’s NOT expensive either.
My point is simply that it’s not optically obvious to me that the straddle is expensive by noticing that it is priced at the maximum value of either of its legs.
If the structure is not trading near its maximum value, you are simply back to wondering if the thing that drives your eventual P/L is cheap or expensive and that thing is the unknowable relationship between the implied volatility and the realized volatility during your holding period, whether short or long.
- Does the maximum price of the straddle depend on the expiration date?
- The stock price
- The strike price
Answer
No
Go back to the answer to #1. There is no reference to volatility or time inputs in the computations. The arbitrage bounds of max value depend only on:
In fact at the extreme, where an option is worth its maximum value, that's the same world where time or volatility is infinite. The option’s model value will simply explode until it reaches its arbitrage bound. And as we saw those values are in fact quite bounded, finite, and easily calculable.
- From August 5th, 2022 until January 11, 2023, when I’m dissecting this, CVNA has fallen from $46.98 to $5.50. It lost nearly 90% in about 5 months or 109 business days. On August 5, 2022 the LEAP (Jan2024 expiry) $50 strike call was marked at $20.65 Use put-call parity to compute what price we sell the straddle for.
Answer
We have the call price so we must compute the equivalent put price to arrive at a straddle. If the put price trades for any price other than what’s implied by put-call parity then there is an arbitrage so this is not only a valid thing to compute, but the price you can expect to find in practice (in reality carry costs will matter).
50 strike Put = Intrinsic + 50 strike Call - Carry Cost
50 strike Put =$3.02 + $20.65 - 0
50 strike Put =$23.67
50 straddle = 50 strike call + 50 strike put
50 straddle =$20.65 + $23.67
50 straddle =$44.32
We sell the $50 strike straddle at $44.32
Fast forward to January 11, 2023 the $50 strike call is marked at $.35 and CVNA is $5.50
Use put-call parity to compute what price is the straddle marked at.
Answer
Once again we must compute the value of the $50 strike put from the knowledge that the call is marked at $.35
50 strike Put = Intrinsic + 50 strike Call - Carry Cost
50 strike Put =$44.50 + $.35 - 0
50 strike Put =$44.50 + $.35 - 0
50 strike Put =$44.85
50 straddle = 50 strike call + 50 strike put
50 straddle =$.35 + $44.85
50 straddle =$45.20
The $50 strike straddle is marked at $45.20
- What’s my p/l if I sold the straddle naked?
Answer
On August 5th, 2022 we sold the straddle at $44.32
On January 11th, 2023 the straddle is marked at $45.20
Our net P/L is $44.32 - $45.20 = -$.88
We sold a straddle. 109 days out of its 532 days of life elapsed and it’s worth more than we sold it. It’s a bit banal to point this out…we sold a straddle naked, the stock made a giant move and we lost. If the stock rallies from here we will recoup losses and even make money — but that’s because we are short a deep in-the-money put so we have a long delta or synthetic long position in the stock. This doesn’t have much to do with the option anymore, if we want that exposure we could simply liquidate our straddle and buy the stock. The volatility damage is done.
Using the daily call marks from August 5, 2022 until January 11, 2023 I computed a daily straddle mark. This was the p/l path of selling 100 CVNA Jan2024 expiry $50 strike straddles using daily closes.
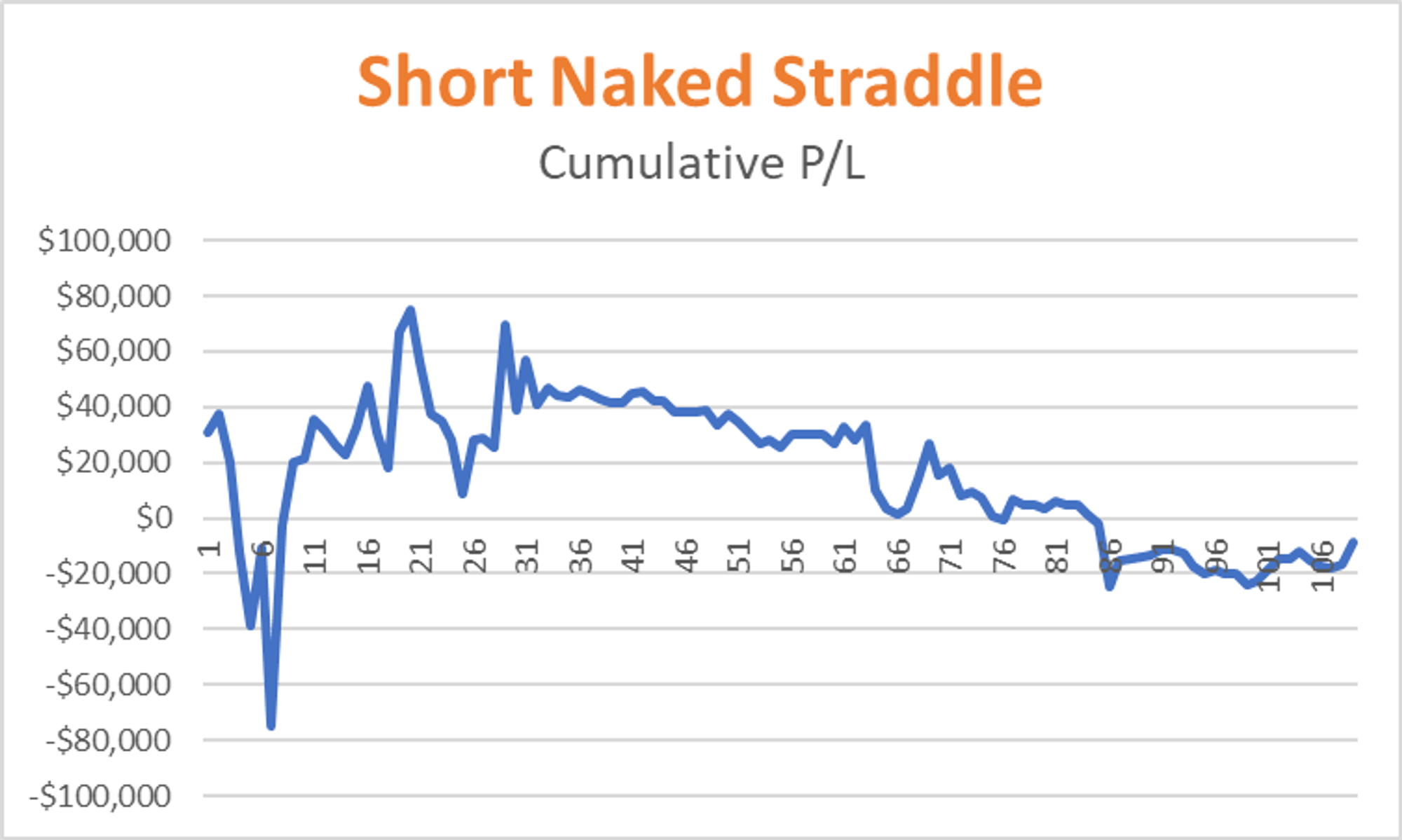
This is just the beginning of the questions we can ask. Let’s continue.
- Now let’s imagine we delta-hedged the $50 strike straddle when we sold it. Do not use an option model for the following questions. Start with your intuition. (This is a general learning technique — try to solve the problem with what you know first. Then when seeing how it’s done, it will stick. If you jump straight to the answer your mind will nod along, you will presume your intuition would have matched the correct method, and you will not have actually retained the new information.) ✍🏾Write your answers to the following on a piece of paper:
- First of all, do you think we bought or sold shares of CVNA to delta hedge? [In other words, did the straddle have a positive or negative delta. Hint: a straddle delta is the sum of its constituent call delta and put delta. Remember that put deltas are negative]
- Guess the magnitude of the delta.
- True or False: I made more money by delta-hedging once at the initiation of the short straddle than if I sold it naked?
- If you don’t have experience with longer-dated or high volatility options, the intuition can be devilish. In fact, the answers you estimate to the above question might be very wrong. If you are inexperienced but have read Lessons From The .50 Delta Option, you have a chance. Let’s start hacking away at this. Use an option calculator (the European model here is fine) to compute the $50 strike call. To get the $50 strike call to match the mark of $20.65 on August 5th, 2022 recall our assumed inputs:
- This is a “high” volatility name
- This is a “long-dated” option
DTE: 532
Strike: $50
CVNA price: $46.98
Rates and Divs: 0
…and an implied volatility of 100.6%
These inputs will yield a call price of $20.643 (close enough to our desired $20.65)
Now, instead of using intuition from question #5, let’s calculate the answer. What is the delta of the $50 strike straddle?
Answer
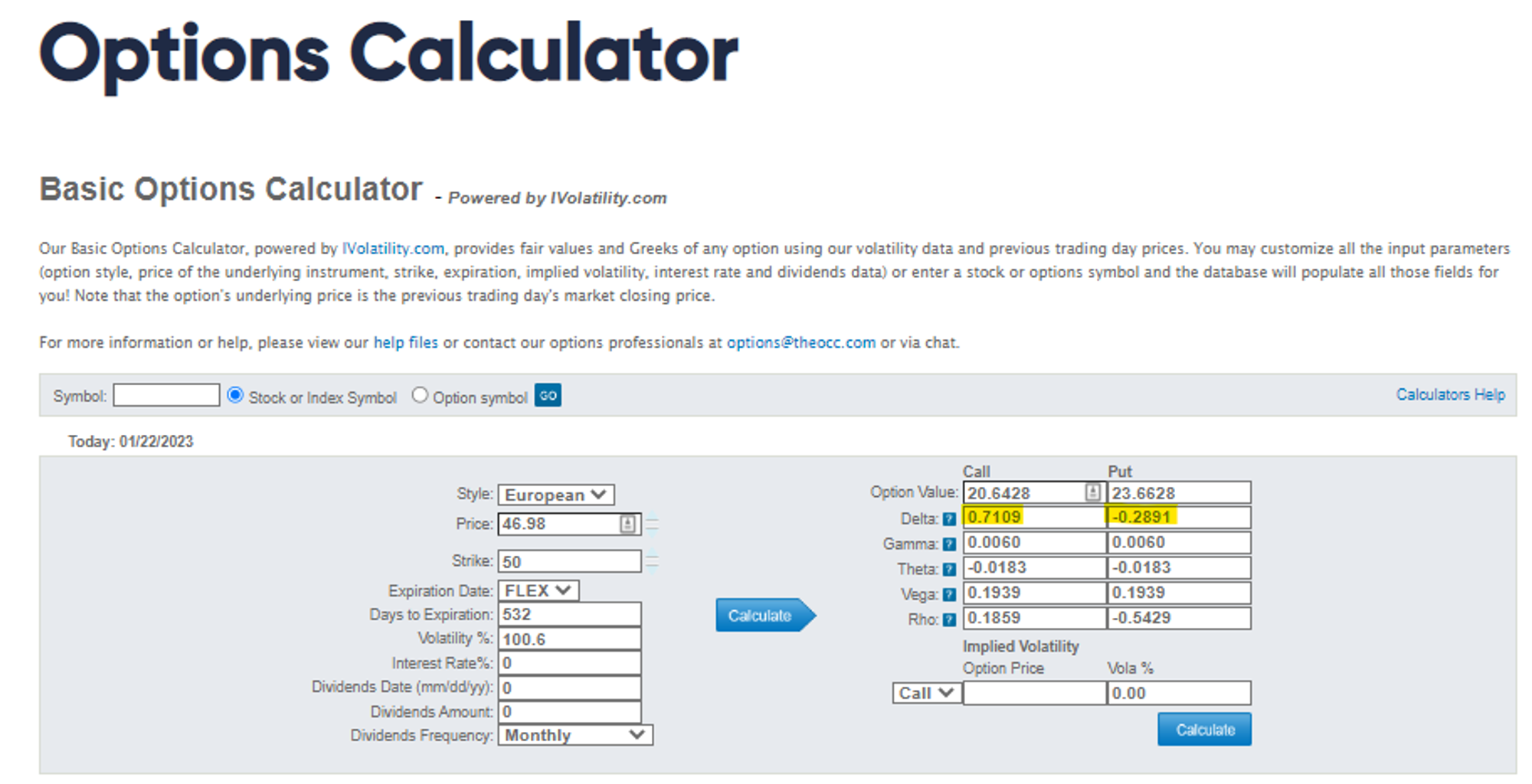
The $50 strike call has a .71 delta
The $50 strike put has a -.29 delta
The straddle delta = .71 + (-.29)
The straddle delta = .42
The straddle has a .42 delta! Not only is the straddle delta positive it’s not dissimilar to the rule of thumb that “an at-the-money call has about a .50 delta”!
The call, which remember is slightly out-of-the money (strike = $50, stock price = $46.98), has a .71 delta!
This is not surprising to experienced traders because the rule of thumb fails in 2 conditions and both are present here:
Again, the full explanation can be found in Lessons From The .50 Delta Option
- Recall that we used the $50 strike call mark of $20.65 to imply a straddle price of $44.32 on August 5th.
- Assume you sold 100 CVNA $50 strike straddles on August 5th and hedged on the straddle delta we computed in question #6.
- Assume we only hedged once at the initiation of the trade.
What’s your cumulative p/l as of January 11, 2023?
Answer
From question #4, we know we lost $.88 on the straddle mark
We sold 100 straddles and hedged them on a .42 delta which we computed in question #5.
💻Computations: How many shares did we buy to hedge the straddles?
A positive delta means that if the stock price rises, an option structure increases in value. So to hedge a positive delta option structure that we sell, we must buy shares to neutralize our p/l from stock price movements.
In other words, delta is a hedge ratio. If the stock goes up $1, the straddle increases by $.42.
If we delta hedge at the inception of the trade we must compute how many shares to buy as follows (recalling that a single option contract corresponds to 100 shares, the multiplier):
Hedge ratio in shares = 100 straddles x .42 x 100 multiplier
Hedge ratio in shares = 4,200 shares
So we need to buy 4,200 shares for $46.98 at the initiation of the trade.
Unfortunately, on January 11, the stock price is $5.50:
Share P/L = 4200 x ($5.50 - $46.98) = -$174,216
Straddle P/L = -$.88 x 100 straddles x 100 multiplier = -$8,800
Total P/L = -$183,016
- I’m guessing the answer to question #7 was disturbing. Option sellers might be objecting in several ways
- “Why would I hedge just once at the inception of the trade?!”
- “Why would I hedge on such a heavy delta?”
My response
“Why would I hedge just once at the inception of the trade?!”
“Why would I hedge on such a heavy delta?”
If we recall the original tweet, it caveated the trade thesis with “if you can hedge the upside blowout risk”. One of the ways you can hedge the upside is to buy shares of the stock while being short the straddle. In fact, this is a counter to the second objection — maybe with what we knew at the time we should have hedged on an even bigger delta than .42.
Yes, our downside p/l would have been EVEN worse but going into the trade it was the upside that the straddle seller was nervous about!
An experienced option trader would reply, you can’t use shares that have linear p/l to hedge all aspects of options that have convexity as their deltas change. This is 100% correct.
So what are we to do?
Well, the only real way to hedge a short option is to…buy another option. And therein lies the problem — we thought the options were very expensive to start with (optically at least) so now we are going to be picking and choosing which to sell and which to buy?
This is getting hard pretty fast. I mean, we can see just how sensitive our p/l is to the delta we hedge on . If we acted as if the call and put were both .50 delta, the straddle would have zero delta and we just sell the straddle naked. The higher the delta we assign to the call, the worse our p/l is when the stock drops 90%.
As you start thinking about the possible futures, like the one where the stock doubles instead of losing 90% you that your p/l is very sensitive to the vols you put in the model because the deltas depend on them.
- I addressed the caveat of hedging just at inception in #8. But by now, you are hopefully starting to build the intuition that the performance of an option trade depends on how much the stock moves and how fast. In other words, its realized volatility. We will open Pandora’s Box, by discussing one last approach to selling this straddle. Thus far we have seen that the lived experience of selling this straddle naked was a small loser, and selling it with a delta hedge at inception, was a giant loser. We can also hedge our straddle every day.
- As the stock moves, the delta of the straddle changes. When the stock goes up, the straddle delta grows beyond the delta we initially computed. To stay market neutral, we need to buy shares.
- As the share price falls, the straddle delta becomes more negative. Since we are short the straddle our exposure gets longer. This means we need to sell some of the shares we initially bought (or possibly short the stock).
- naked (no hedging)
- hedging once at the inception of the trade
Gamma Scalping
These constant changes in the delta of our position is what is commonly referred to as — gamma. So whether or not you are delta-neutral, if you are short a straddle you are always short gamma. Which means you will be buying shares high and selling them low. If the stock doesn’t move around too much compared to the price of the straddle you sold then you won’t book too many of these “negative gamma scalp” trades.
This dynamic is the yin and yang of options. If you sell an optically expensive straddle, but the stock moves a lot the sum of these negative p/l stock trades will overwhelm the premium you sold over the life of the trade. If the stock doesn't move around too much compared to the price you sold the straddle at, then you will have a winning portfolio.
From August 5th to January 11th, I grabbed daily closing prices for CVNA stock and options. This allowed me to reconstruct the implied volatility and therefore delta of $50 strike calls.
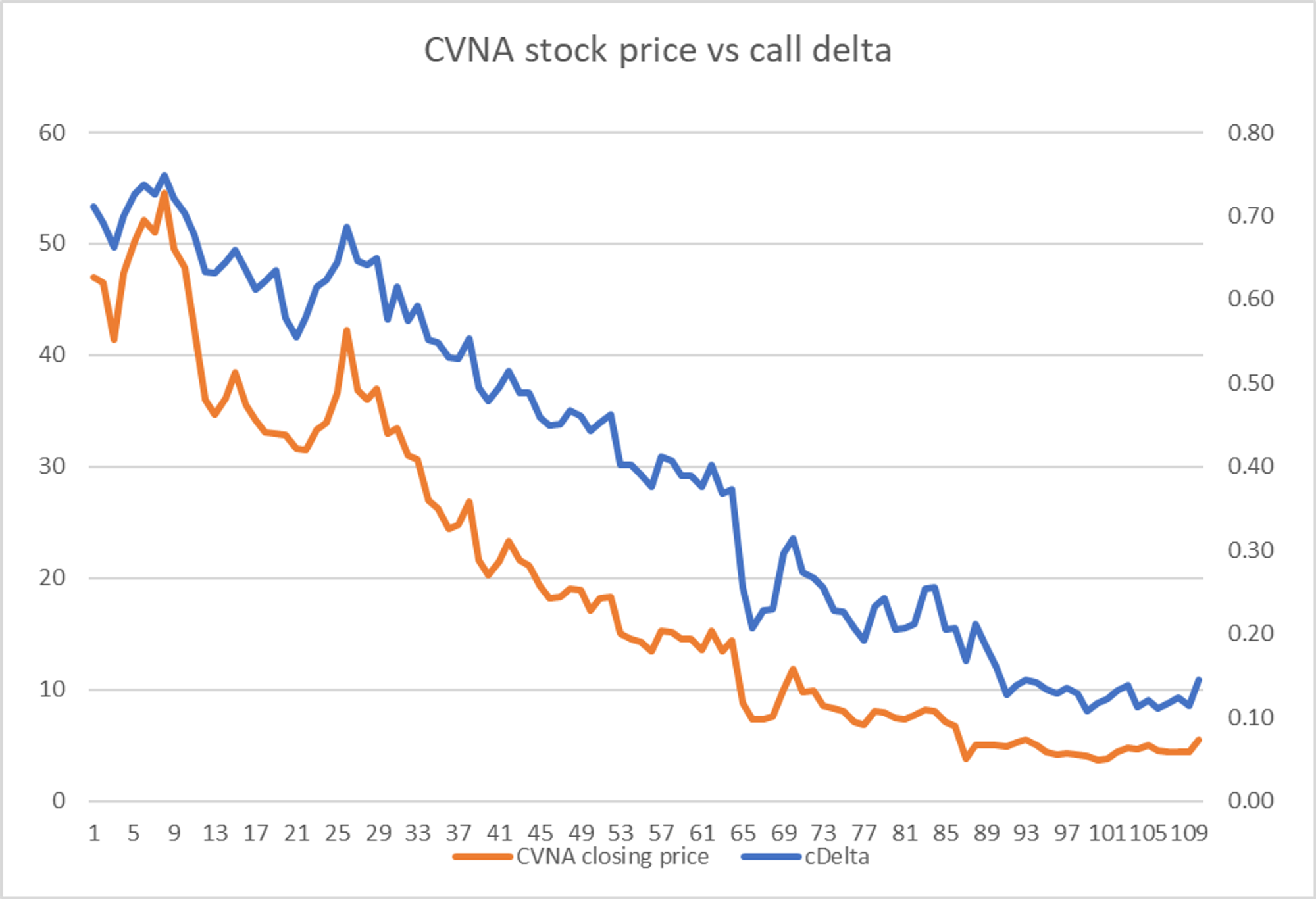
You can see the stock’s price path. As expected, the delta (right axis) of the $50 strike call has fallen as it went further out-of-the-money.
Every time CVNA falls, the deltas fall and you need to sell shares to maintain a neutral exposure to the underlying. If your thesis is that the option implied volatility is high you want to isolate the bet to how much CVNA bounces around and not directional exposure to its price.
If you could rebalance every second and there were no gaps or overnights you could do this, but transaction costs and discontinuities in liquidity mean you can only rebalance to neutral on discrete intervals.
A textbook interval is to hedge daily at the close. If you were able to trade at the closing price with no slippage, your lived realized experience of volatility would match “close-to-close” volatility.
If you hedge at other intervals, you are sampling a different volatility than “close-to-close”. That’s why realized volatility can be some number, call it 90%, but 2 people with the same option position can experience totally different p/l paths. Maybe I hedge at the open every day and therefore sample a volatility of 110%. If I’m long implied volatility of 100% then I win. You are short the same volatility at 100% but hedge your deltas at the close. You also win.
But if I hedge at the close and you hedge at the open, then we both lose!
When to hedge and what implied volatilities to use to impute your deltas is a rabbit hole as deep as its Alice In Wonderland namesake. But you can use intuition to see how daily hedging would have stacked up against the 2 extreme examples we worked through:
How do you think the p/l performance of daily hedging would have fared vs these 2 other cases?
My answer
From question #6, we know on August 5th, CVNA 50 strike straddle implied 100.6% volatility. That corresponded to an initial straddle delta of .42
Since the price path was mostly down and the call delta peaked in the early part of the trade we were likely carrying less than the 4,200 shares so I would expect that daily hedging would have been better performance than initiating a hedge and never re-balancing. But I wouldn’t expect it to be as good as not hedging (ie the naked straddle case) since we carried a long share position until the call delta dropped below .50 about 2 months into the holding period.
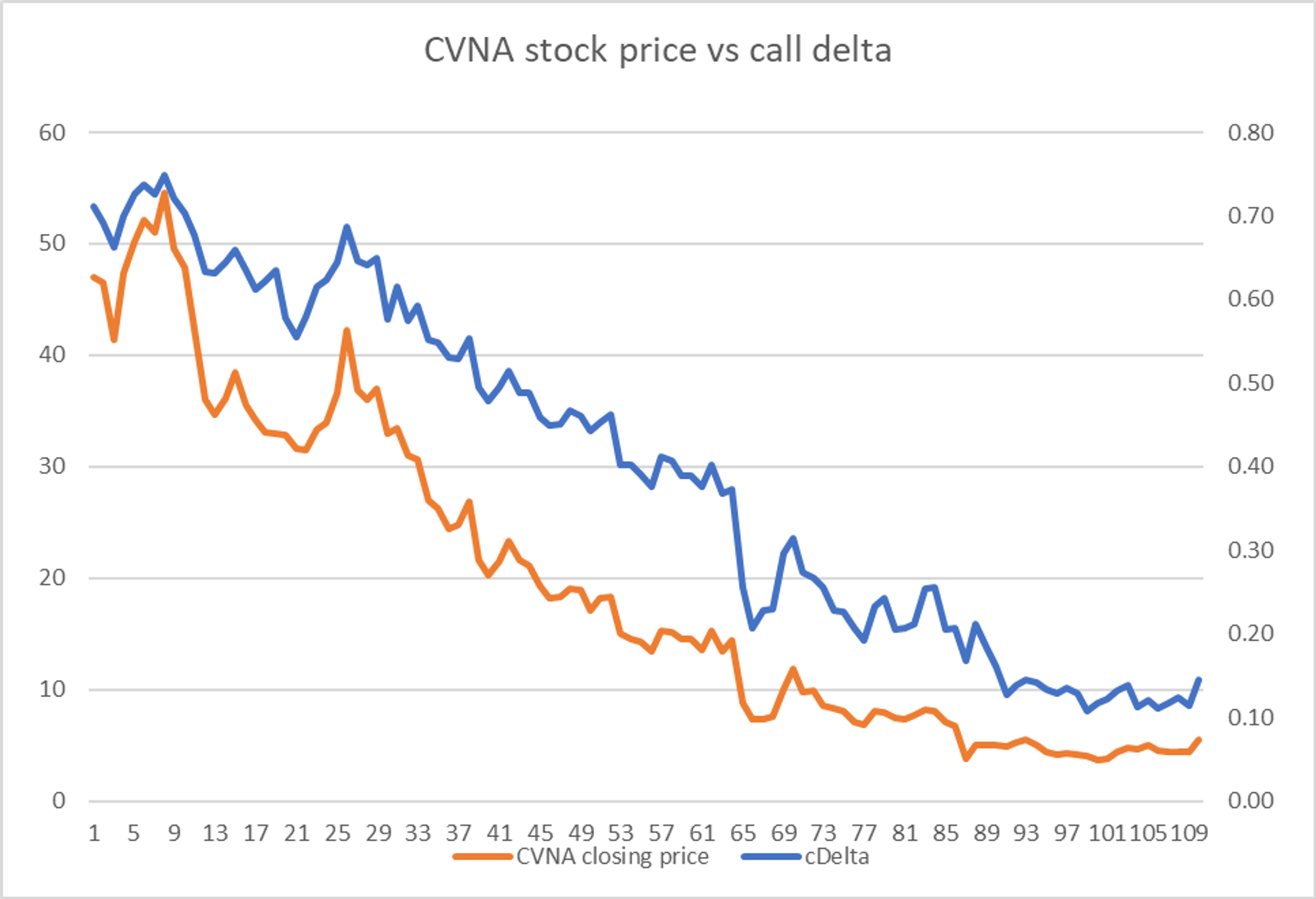
It’s true that we were short shares for the past four months, but this wasn’t enough to offset the “buying high” / “selling low” negative gamma effect because the stock was simply too volatile.
And this is the heart of the matter.
If we compute daily close-to-close volatility [using an annualization factor of sqrt(252 business days)] we get a realized volatility of 182% from August 5th to January 11th. Remember we sold this straddle at 100% implied volatility!
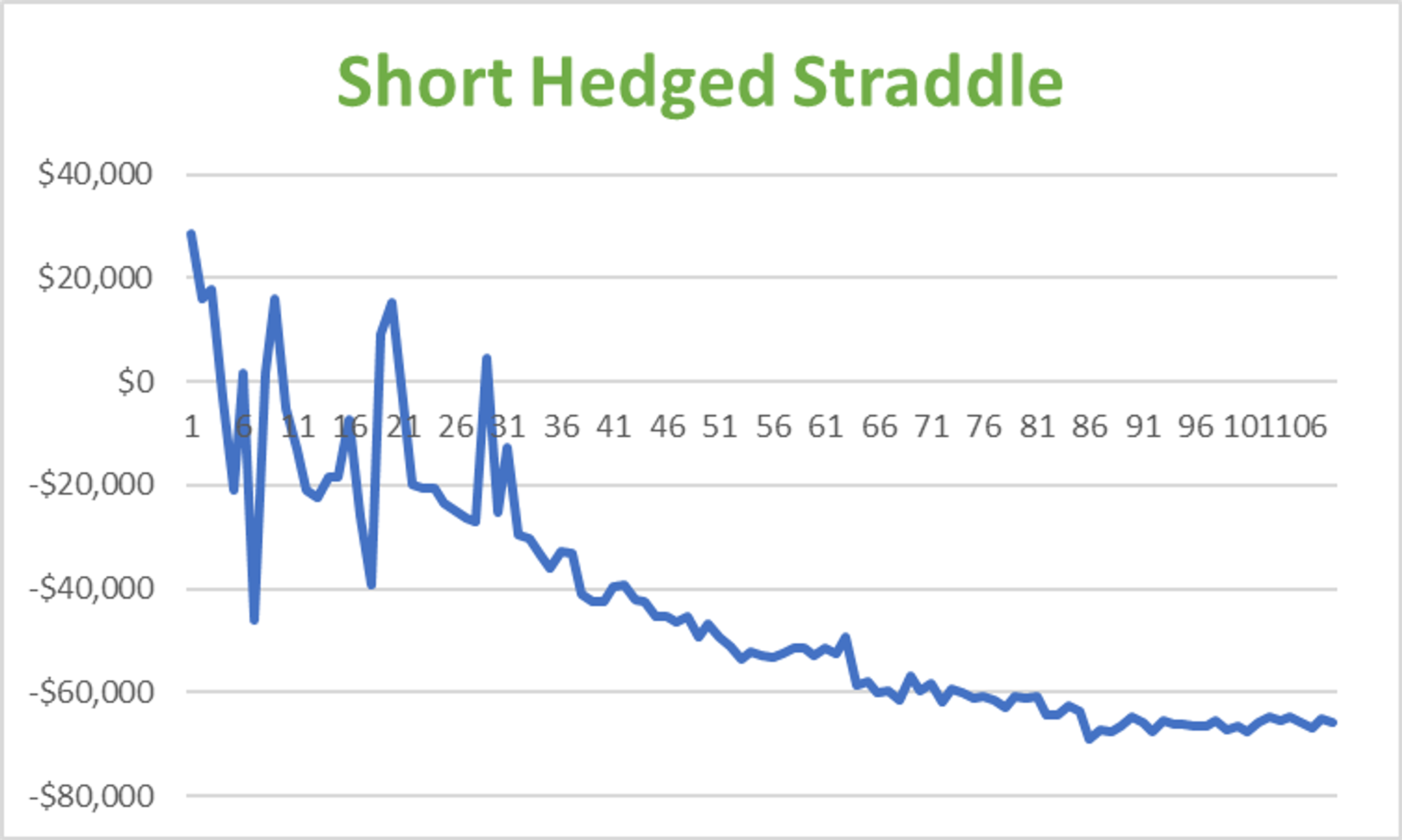
So what was the p/l if we hedged our deltas at the close (deltas are imputed by the daily IV marks on the $50 strike)? Assume 100 straddles again.
I did the calculations for you in a sheet that looks like this:
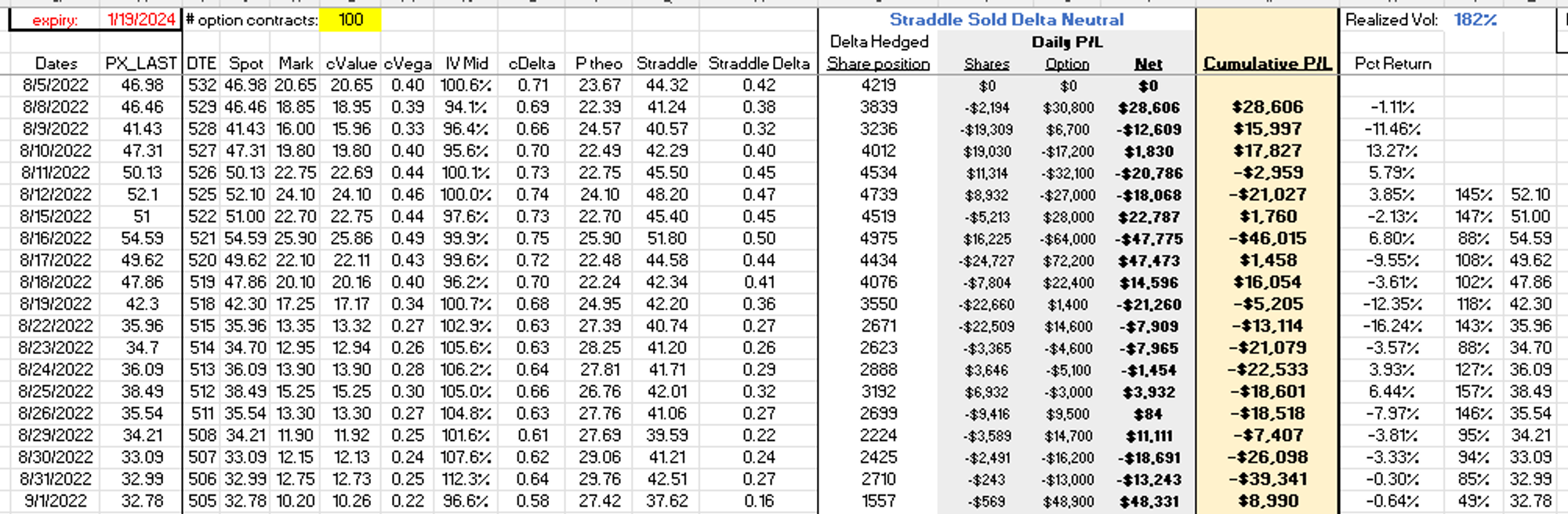
Cumulative share trading P/L : -$56,856
Naked straddle P/L from question #4: -$8,800
Net portfolio P/L: -$65,656
Worse than selling the naked straddle, but much better than hedging the initial delta and letting it ride to “hedge the upside risk”
Wrapping Up
Hedging and trading options is an art. Which risks are you willing to take? What parameter are you trying to isolate? In hindsight, the CVNA 100% vol straddle for 18 months was actually cheap not expensive. Relying on optics is dangerous. In fact, I could see the logic making me want to do the opposite trade — this is a turd stock that could be worth zero or turned into a GME-style football. The risk premium embedded in this option accrues to its buyer because nobody wants to be an opening long of this option because it looks “high”. If you bought this straddle and hedged it once or daily it was a mirror image of the seller’s losing position (which means buying the straddle naked was also close to a scratch, it was just a modest winner).
Aside: Sucker’s Bets
I spent a lot of my career buying optically “expensive” options because they were still trading well below realized. See: The “No Easy Trades” Principle and Distributional Edge vs Carry. Optics should lead you to explore the opposite of your gut reaction. In sports, they call it a sucker’s bet when a line looks obviously mispriced.
And if you doubt it’s an art consider the following conundrums:
The higher the implied vol we use the higher the delta of an out-of-the-money option. So the higher the implied volatility we observed on the $50 strike call, the more long shares we would hold as a hedge in this instance. If you hedged on a lower vol your p/l would be better (take the statement to the extreme and your performance matches the naked straddle).
But if anything these options were too cheap and you could argue that you should hedge on a higher vol, but of course, your p/l would be even worse. Furthermore, if you could have sold the straddle on a higher vol, you would have hedged on higher deltas. So you would have earned more P/L for selling the straddle at higher volatility but incurred more losses on the daily hedging.
Do you hedge on the implied delta? Do you adjust your deltas for spot/vol correlation? The lognormal assumption in the B-S model has a tyrannical impact on deltas. The further an asset’s distribution is from lognormal the worse the model’s delta estimates will be. Remember deltas are your share hedge ratios and the number of shares you choose to buy or sell all day, every day is a giant piece of this whole business of options trading.
(The most concise recipe I have for trading options profitably is “be short the options where the stock’s going and long where it ain’t”. This is the opposite instinct that most people have when they approach options. They want to sell options because “the stock ain’t going there”. They have yet to learn to step through the daily management of an options portfolio.)
The p/l of a delta-hedged position depends on the implied vol you are long or short because it not only affects the option premium but the hedge ratios you rely on every day. The inevitable mismatch between the implied vol with the realized vol means you are never perfectly delta hedged and your p/l is going to depend on how much the stock moves when precisely when you are mismatched (ie not neutral).
This is rolling weekly volatility (displayed in annualized volatility) vs CVNA stock price for the holding period.
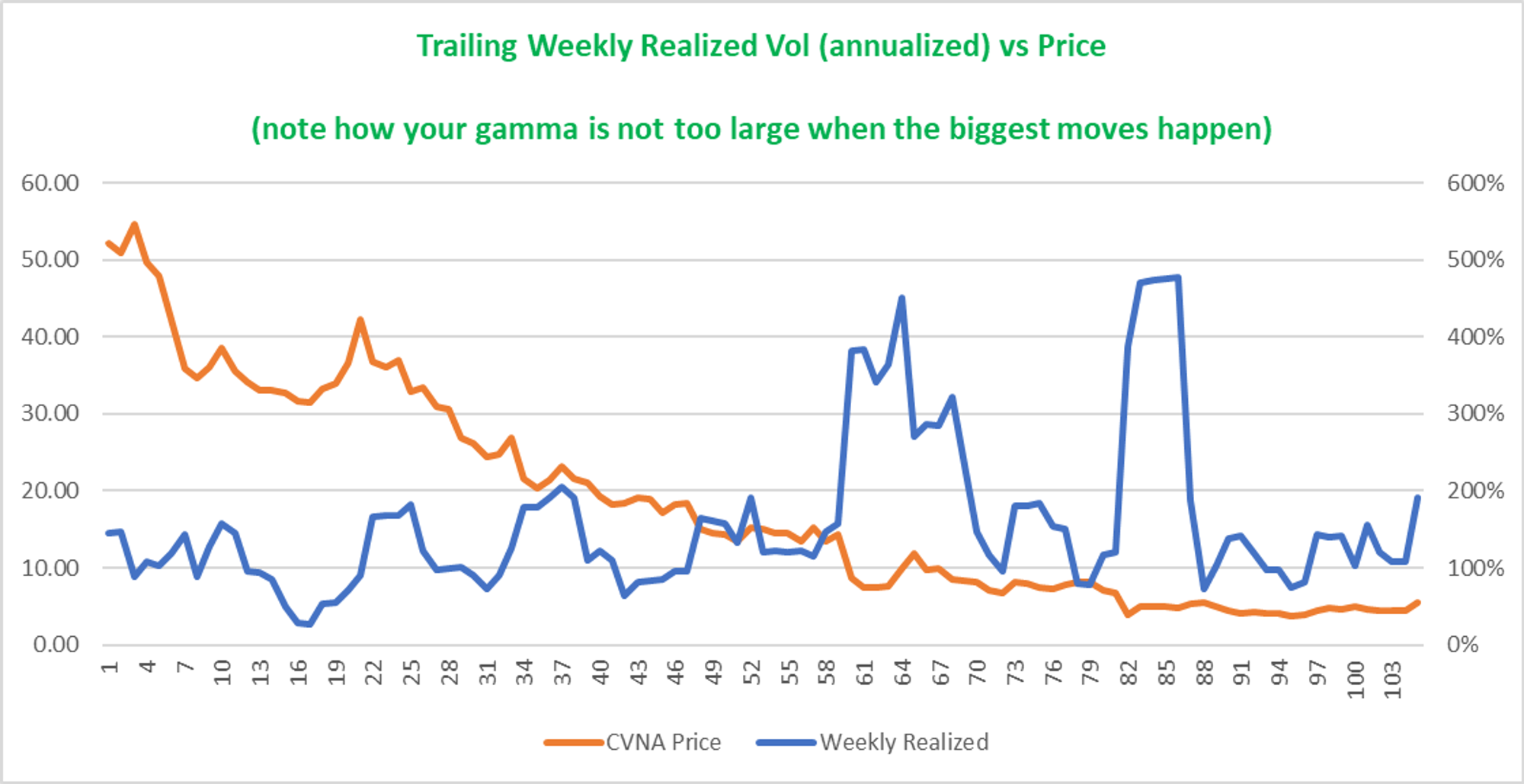
More than 70% of weeks experienced higher than the 100% implied volatility the straddle seller is short. The median weekly volatility is 123%. One bit of salvation is that those 2 giant spikes in realized volatility occurred when the $50 strike was 100 to 200% out-of-the-money. Meaning it was already lower in delta and gamma than a near-the-money option which meant the negative gamma scalps were not as bad as they could have been.
You can see the p/l volatility calm down as the short options get further OTM, spitting off less Greeks to rebalance:
Bonus Question: Instead of selling 100 straddles, imagine you sold 100 of those $50 strike .71 delta calls and hedged them daily. How do you think the p/l performance would compare to the short 100 straddles hedged daily?
Answer
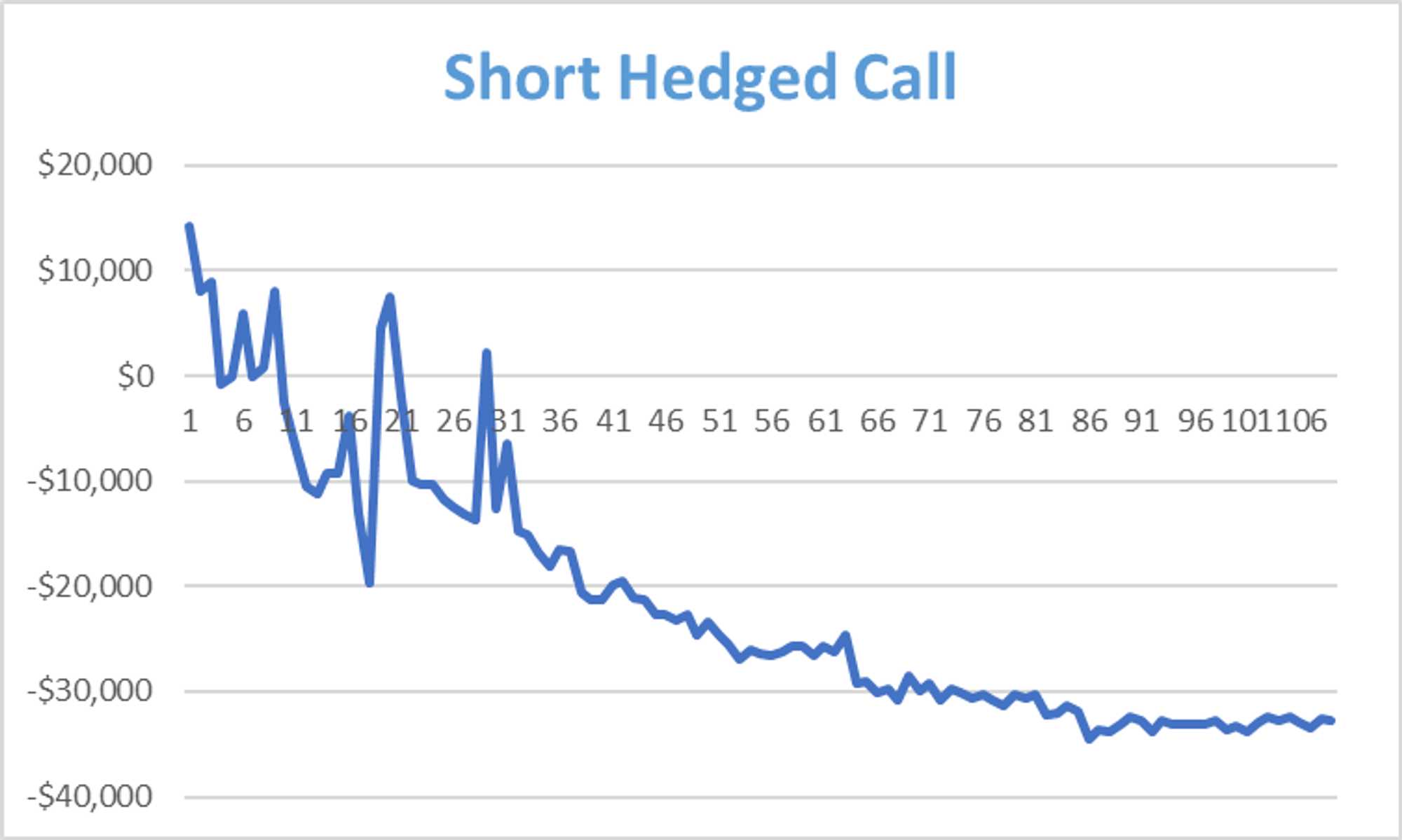
The short call performance is half of the straddle performance.
Why?
Put-Call parity!
Remember if I’m long 100 calls and sell 10,000 shares against them I have turned them into synthetic puts. If I instead sold only 5,000 shares then I have turned the position into long 50 straddles.
I’m long 50 calls and long 50 synthetic puts = long 50 straddles
If you are short 100 calls delta neutral it is very similar to being short 50 straddles neutral. In fact, option traders don’t usually care about how many calls or puts they have on a strike (unless pin risk is possible). They just care about the net options on the line!