Logic
- If A is married and looks at B and B looks at C who is unmarried, is a married person looking at an unmarried person?
yes
no
can’t tell
Solution Yes
Whether B is married or unmarried a married person is looking at an unmarried person
- You have 3 coins. 1 weighs less than the rest. Can you find it with just 1 weighing?
- Divide the three coins into two groups of one coin each, and leave the third coin aside.
- Place one coin on each side of the balance scale.
- If the scale balances, then neither of the two coins on the scale is the lighter one, meaning the coin you left aside is the lighter coin.
- If the scale does not balance, the side that goes up (the lighter side) contains the lighter coin.
Solution
To find the lighter coin among the three coins with just one weighing, you can use a balance scale and follow these steps:
There are two possible outcomes from this weighing:
This method ensures you can identify the lighter coin among the three with just one use of the scale.
- 10 red socks, 10 blue socks. How many to pull for matching pair? How many to pull for 1 of each?
Solution
3 and 11 respectively
- If you have 3 you have 3, if you have 2 you have 2, if you have 1 you have none. What is it?
Solution
Choice
Arithmetic
- Dinner cost $60 including a 20% tip. How much was the meal?
Solution
1.2x = 60
x = 50
- I'm 3x your age today. In 3 years I'll be twice your age. What are our ages?
Solution
y = 3x
y + 3 = 2(x + 3)
3 and 9
- A bat costs $1 more than a ball. Together they cost $1.10. How much do they each cost?
Solution
ball = .05, bat = 1.05
- What's bigger the square of an average or the average of the squares?
Solution
average of the squares
- Cigarette question: A miser can make 1 cigarette from 5 cigarette butts. What is the maximum number of cigarettes the miser can make from 1000 cigarette butts ?
Solution
he first makes 1000/5 = 200 cigarettes which gives him 200 butts in the end
then he has 200 butts to make 200/5= 40 cigarettes which gives 40 butts
again he has 40/5 = 8 cigarettes which gives 8 butts
8/5 = 1.6 but he makes only 1 cigarette of that.
3 butts remain in the end - useless (as he cant make a cigarette with 3 butts)
Total cigarettes made = 200 + 40 + 8 +1 = 249 cigarettes
- You drive to the store and back. The store is 50 miles away. You drive 50mph to the store and 100mph coming back. What’s your average MPH for the trip?
Solution
66.66 mph
(1 hour going and 30 minutes returning)
- You drive 1 mile at 30mph, how fast do you have to drive the second mile to average 60 mph for the trip?
Solution
Can't be done. The first mile took 2 and to drive 2 miles at 60mph you must complete the trip in 2 min
- Solve without a calculator:
Solution
We can then realize that:
So we can substitute as our target instead of just :
The target is simply
= 243
So in the original equation x = 243 or -243
Probability & Stats
- If 10% of population is left handed and 1% of women are left handed, what percentage of men are left handed? (assume equal amounts of men and women in the population)
Solution
.5 women are left handed
9.5/10 left handed people must be men
9.5/50 = 19% of men are left handed
- Expected Value
- coin toss game
- Insurance on a iPad
- Roulette wheel
- 2 pointer vs 3 pointer
- Getting a blackjack from a full deck
EV of:
Divisibility Rules
- Divisible by 10 if ends in 0
- Divisible by 2 if even
- Divisible by 3 if digital roots is 3
- Divisible by 4 if the last 2 digits of a number are divisible by 4
- Divisible by 5 if the last digit is divisible by 0 or 5
- Divisible by 6 if it's divisible by 3 and even
- Divisible by 7 if the difference between twice the unit digit of the given number and the remaining part of the given number should be a multiple of 7 or it should be equal to 0
- Divisible by 8 if the last 3 numbers are 000 or last 3 are divisible by 8
- divisible by 9 if digital roots is 9
Misc Topics
- Richter scale as log scale. A 6 is 1000x a 3 not 2x
- Socratic lesson: Teaching about mean absolute deviation (easier than variance) MAD and daylight savings time Daylight savings time causes accidents but how do we know?
If CA averages 100 car accidents a day, then would you be surprised if there was 92? 105? 300?
There's an implicit level of “surprise”
Compute MAD by averaging the distances of each day’s accidents from 100. The more a sample exceeds the average the more likely there result is not random
- Triangle method for summing the numbers from 1 to N
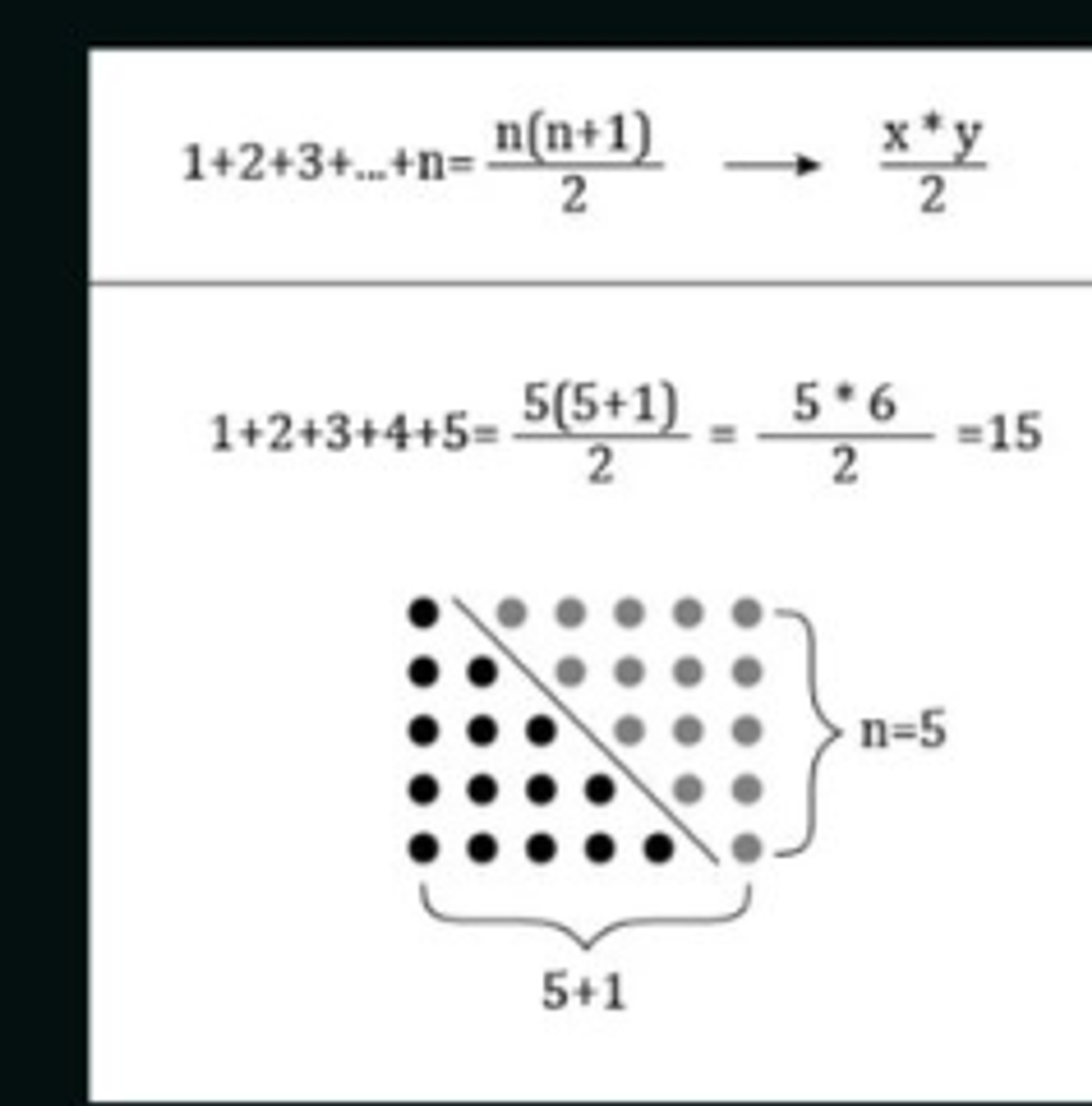
- Passphrases > passwords
Passphrases: hard for computer to crack (compute time for long strings) and easy for human to remember vs
password: easy for computer to crack hard for human to remember
- Sum of finite geometric series
- derivation
- socratically show terms in the sequence
- set equal to the same sequence times r
- solve for Sn
- Depreciation: When an asset depreciates by a constant percentage each year, the total value lost over a number of years can be calculated as the sum of a geometric series.
- Loan Payments: The formula for calculating the remaining balance of a loan involves a geometric series when the loan is being repaid in equal installments over time.
- Investment Growth: The total value of an investment over time that receives a constant rate of interest compounded annually can be modeled as a geometric series.
- Electronics: In a resistor-capacitor (RC) circuit, the voltage across the capacitor or the charging and discharging of the capacitor can be described by a geometric series.
- Computer Science: In algorithms, particularly divide and conquer algorithms like the binary search, the time complexity can often be expressed as a geometric series.
- Physics: In certain problems in physics, such as calculating the total distance covered by a bouncing ball where each bounce is a fraction of the height of the previous bounce.
- Acoustics: Echoes can be thought of as a geometric series, where each successive echo has a smaller amplitude than the previous one
applications
Real-life examples of summing a finite geometric series include: